|
SONLU ELEMANLAR YÖNTEMİ İLE STATİK ANALİZ
- Giriş
Bu çalışma, 2 serbestlik derecesine sahip kiriş
elemanlarla birbirine bağlanmış bir sistem üzerinde meydana
gelen deformasyon ve gerilmeleri dağılımı tespit
edilebilmesi amacıyla yapılmıştır. Burada çözüm yöntemi
olarak, Sonlu Elemanlar Metodu kullanılmıştır.
Sonlu Elemanlarla Yöntemi ile problemin çözümünde
izlenilen adımlar aşağıda belirtilmiştir.
Sonlu elemanlar ağının oluşturulması
Her bir eleman için direngenlik matrislerinin oluşturulması
Tüm yapıya ait direngenlik matrislerinin bulunması
Sınır koşullarının tanımlanması ve
kuvvet vektörünün bulunması
Elde edilen denklemlerin çözülerek sonuçların elde
edilmesi
2. Modelleme:
Şekil 1 de görülen kiriş sisteminde, her iki
mafsal arasındaki mesafede tek bir eleman olacak şekilde çözüm
yoluna gidilmiştir. Bu sebepten dolayı oluşan hata göz ardı
edilmiştir. Eleman uzunluğu genişliğine göre 1/10 oranından
çok fazla olduğu için kullanılan yöntemlerden kaynaklanan hatalar
kabul edilmiştir.
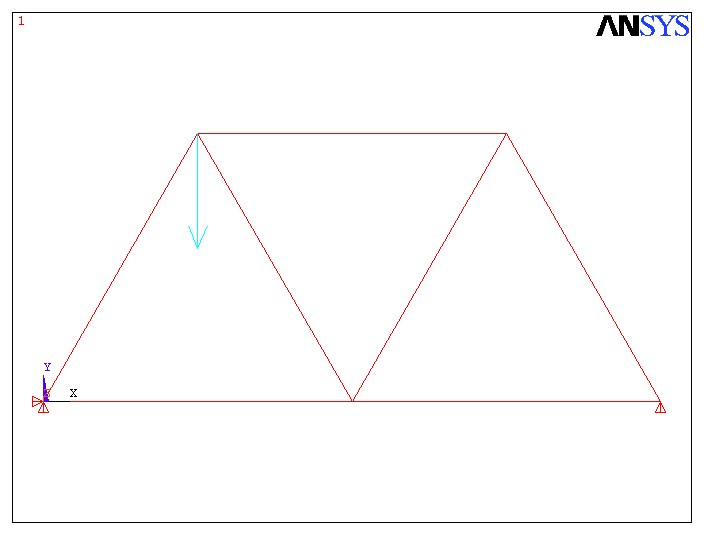
Şekil 1. Kiriş Sisteminin Sonlu Elemanlar Modeli
Elemanlara bölünen sistemin birbirlerine bağlanması
Şekil 2 de gösterilmiştir. Çözüm sırasında Şekil
2deki eleman ve düğüm numaraları göz önüne alınarak
hesaplama yapılmıştır. Şekildeki sistem 2 serbestlik
derecesine sahip 7 tane elemandan ve 5 tane düğüm noktasından
meydana gelmektedir.
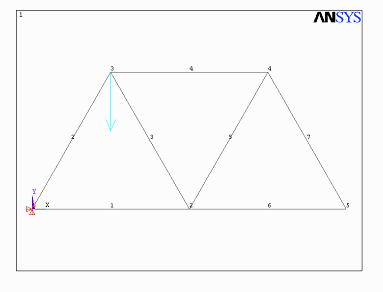
Şekil 2. Kiriş Sistemi Üzerinde Kullanılan
Eleman ve Düğün Noktalarının Yerleri
Burada yapılacak analizler
için kullanılan malzeme özellikleri Tablo-1de gösterilmiştir.
Tablo 1. Malzeme Özellikleri
| |
Değeri
|
Birim
|
|
E (Elastisite Modülü)
|
2.1 E11
|
N/ m²
|
|
n (Poisson
Oranı)
|
0.3
|
-
|
Kirişlerin boyutları is e;
L = 1 m (Kiriş uzunluğu)
D = 20 mm (kiriş çapı)
- Her bir eleman için direngenlik matrislerinin oluşturulması
Bu aşamada her bir elemana ait direngenlik matrisleri çıkarılmıştır.
Bu denklemlerin çıkarılmasında 1 numaralı denklem kullanılmıştır.
 ( 1 ) ( 1 )
F : Kuvvet matrisi
K : Direngenlik matrisi
U : Yer değiştirmeler matrisi
g : Global eksen takımını
ifade eden sembol
Kiriş elemanlar için elde edilen genel kiriş denklemi 3 numaralı
denklem ile verilmektedir.
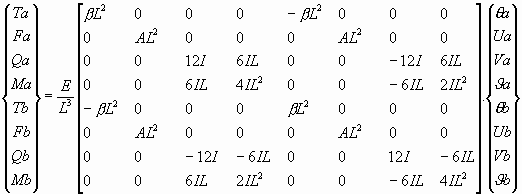 ( 3
) ( 3
)
3 numaralı denklem her bir elemanda 2
serbestlik derecesine (x ve y yönlerinde ötelemeye sahip) elemanlar için düzenlenirse;
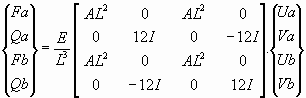 ( 4 )
( 4 )
bütün elemanların boyutları
ve uzunlukları birbirine eşit olduğuna göre, 7 eleman içinde
kendi eksenlerine göre oluşturulacak direngenlik matrisi de birbirinin aynı
olacaktır (tablo 2).
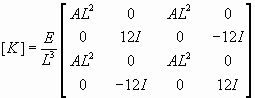
konumu gereği global eksene göre oluşan her eleman için
direngenlik matrisleri ise 2 numaralı denklemden;
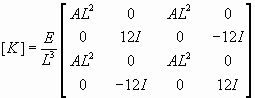
tablo 2. Direngenlik Matrisi
Her bir eleman global eksene göre
farklı bir açı ile bulunduğundan dolayı buların global
eksene göre direngenlik matrislerinin yazılması gerekir. Yukarıda
oluşturulan direngenlik matrisi elemanın kendi eksenine göre oluşturulduğundan,
bu matris global eksen takımına göre yazmak için elemanların x
eksenine göre yaptığı açı göz önüne alınarak T
transpoze dönüşüm matrisi kullanılır. Elemanların x
eksene göre yapmış olduğu açılar tablo 3te
verilmektedir.
|
Eleman Numarası
( i )
|
X ekseni ile yaptığı
Açı ( a )
|
|
1
|
60
|
|
2
|
0
|
|
3
|
300
|
|
4
|
0
|
|
5
|
60
|
|
6
|
0
|
|
7
|
300
|
Tablo 3. Elemanların x Ekseni ile Yaptığı
Açı
Dönüşüm matrisi ise;
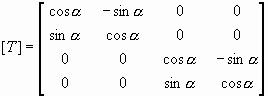
T: Dönüşüm Matrisi
global eksene göre direngenlik matrisi ise;
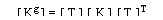 (
) (
)
K : Direngenlik matrisi
T : Transformasyon matrisi
T : Transpoze
İle bulunabilir.
Bu matrislerin çarpımı sonucu oluşan direngenlik matrisleri
tablo 4.1.-Tablo 4.7de görülmektedir.
- Tüm Yapıya Ait Direngenlik Matrislerinin Bulunması
Bir önceki adımda her bir eleman için ayrı ayrı
oluşturulan direngenlik matrisleri bu adımda tek bir matris haline
getirilmiştir. Global eksene göre oluşturulan direngenlik
matrislerinin (tüm sistem için) toplanması sonucu oluşan
direngenlik matrisi tablo 5.te görülmektedir.
- Sınır Koşullarının Tanımlanması ve
Kuvvet Vektörünün Bulunması
Verilen sistemde 1 numaralı düğüm
noktasının x ve y yönündeki serbestlikleri tutulur. Ayrıca, 5
numaralı düğüm noktası kayar mafsal ile bağlandığı
için y yönünde hareket edemez. Bundan dolayı y yönündeki serbestliği
de tutulur. Bu durumda bu kısıtlanmış olan değerler
genel direngenlik matrisinden satır ve sütunları silinir. Oluşan
yeni direngenlik matrisi 7x7 matris boyutlarında olur.
Yapı üzerine uygulanan yük ise 2 numaralı düğüm
noktası üzerinde ve (-y ) yönünde ve 1000 N şiddetindedir. Bu
durum da kuvvet vektörü;
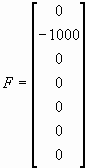
olarak ortaya çıkar.
- Elde Edilen Denklemlerin Çözülerek Sonuçların Elde Edilmes
Sınır şartlarının uygulanmasıyla
genel direngenlik matrisi 10x10 boyutundan 7x7 boyutuna indirgenmiş olur.
Kuvvet vektörü ise 10x1 boyutundan 7x1 boyutuna indirgenmiştir. 1 numaralı
denklem kullanılarak denklem sistemi çözüldüğün de elde edilen
sonuçlar tablo 5te verilmiştir.
Tablo 6 : Yapılan
Analiz Sonucunda Elde Edilen Deformasyon Değerleri
|
