|
Optimizasyon Metotlari
OPTİMİZASYON TEKNİKLERİ
VE SONLU ELEMANLAR PROGRAMI KULLANARAK OTOMOTİV SANAYİİNE UYGULANMASI
Çeşitli yüklere
maruz katı cisimlerde oluşan gerilmeler ve bu yüklerden oluşan
deformasyonlar, geometride meydana gelen değişimler, mevcut yükler altındaki
parçaların güvenli görev yapıp yapmayacağı, meydana gelen deformasyonların
kabul edilebilirliği yüzyıllar boyunca mühendis ve fizikçiler tarafından
analitik yöntemlerle çözmeye çalışılmıştır.
Bu çeşitli yükler
altında model üzerinde oluşan gerilme dağılımı, istenilen sınır değerleri
altında kalması sağlandıktan sonra, mevcut yükleri taşıyacak minimum ağırlık
ve en uygun tasarımın saptanması mühendislik problemleri acısından çok önemlidir.
Bu tip problemler optimizasyon problemleri olarak adlandırılırlar.
Bir problemi formüle
etmek, o problemi çözmek için gereken toplam çalışmaların %50sini oluşturur.
Tasarım optimizasyonunda da problemin doğru formüle edilmesi çok önemlidir.
Bir tasarım problemini tanımlamak icin;
Tasarım değişkenlerini,
Hedef fonksiyonlarını,
Tasarım sınırlamalarını,
tanımlamak
gerekmektedir.
ilk olarak
sistemi tanımlamak için, dizayn değişkenleri olarak isimlendirilen bir değişken
seti belirlenir. Daha sonra bu değişkenlere tahmini olarak sayısal değerler
atanarak sistem oluşturulur.
Bütün
sistemler, kaynaklar, malzeme dayanımı, sistemin cevabı, sistem elemanlarının
boyutları vb. bazı dizayn sınırlamaları içerisinde çalışacak şekilde
tasarlanır. Bu sınırlamalar dizayn değişkenlerine bağımlı olarak tanımlanır.
Eğer bir dizayn tüm sınırlamaları sağlıyorsa, sistem uygun veya çalışabilir
(feasible)dir. Eğer belirtilen sınırlamaları sağlamıyorsa sistem uygun
değildir ve uygun olmayan veya çalışamaz (infeasible) olarak isimlendirilir.
Bulunan uygun dizaynlarından biri kullanışlıdır.
Bütün tasarım
problemleri bir hedef fonksiyonuna sahiptir. Ayrıca, bu fonksiyonların bir çoğu
kesin sınırlamalara sahiptir. Genel matematiksel programlama problemlerinde
tanımlanan çözüm vektörü X*={X1*,
X2*,....,Xn*}, hedef fonksiyonunu
F(X) minimize etmektedir.
Elde edilen bir dizaynın
bir başka dizayndan daha iyi olup olmadığını anlayabilmek için bir kritere
ihtiyacımız vardır. İşte bu kritere hedef fonksiyonu denir. Hedef
fonksiyonu da dizayn değişkenlerine bağlı olarak tanımlanır.
Bu bölümde ise optimizasyon
metotlarının otomotiv sektörüne uygulamaları anlatılacaktır. Bunun için
kamyonlarda kullanılan bir ana makas bağlantı braketinin optimizasyon analizi
yapılarak braketin optimum saç kalınlıkları bulunacaktır.
2. Optimizasyon
Metotları
Optimizasyon
problemlerini çözmek amacıyla kullanılan optimizasyon metotları üç ana başlık
altında toplanmaktadır. Bu metotlar şu şekilde sınıflandırılmaktadır:
- Sıfırıncı Mertebe Metodu
- Birinci Mertebe Metodu
- İkinci Mertebe Metodu
- Sıfırıncı Mertebe Metodu
Sıfırıncı mertebe
metotları, tasarım problemlerinin en basit tipi olarak sınıflandırılabilir.
Bu metotların
avantajları, güvenilir ve kolay programlanabilir olmasıdır. Sürekli devam
etmeyen, yarıda kesilen problemler için çok iyi sonuçlar elde edilmektedir.
Fakat, çok küçük uygulamalar için bile bir çok fonksiyon
istemektedir.
Ayrıca, bu
fonksiyonların oluşturulması uzun zaman aldığından dolayı, bu metotların
üstün yanlarını gölgede bırakmaktadır.
Birinci mertebe
metotları, en çok kullanılan optimizasyon metotlarından olup, birinci
mertebe eğim (gradient) bilgisi istemektedir. Sıfırıncı mertebe metotlarına
göre çok etkili ve uygulanması çok basit olan metotlardır. Eğim (gradient)
vektörü hedef fonksiyonunun türevinden oluşmaktadır. Bu vektörü şu şekilde
gösterebiliriz:
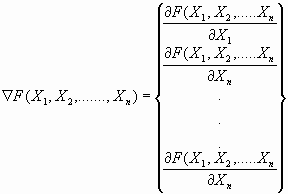
İkinci Mertebe Metodu
(Newton'un Metodu)
Birinci türev sadece
dikey azalma metodunda arama yönünü tayin etmek amacıyla istenmektedir. İkinci
mertebe türev bilgilerinin kullanımı için yakınsama oranı kayda değer
anlamda geliştirilmektedir. Bu metotta bir fonksiyon ikinci mertebe Taylor
Serilerinin genişletilmesi hali olarak şu şekilde yazılır.
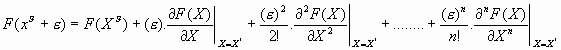
3. Ana Makas Bağlantı
Braketinin Optimizasyon Analizi
Optimizasyon metotlarının
sonlu elemanlar metodu kullanılarak uygulamalarına
Kamyonlarda kullanılan
ana makas bağlantı braketinin optimum saç kalınlıklarını belirlemek amacıyla
optimizasyon analizleri yapılmıştır.
4. Ana Makas Bağlantı
Braketinin katı Modelinin Oluşturulması
Optimizasyon analizinde kullanılacak
olan parçanın katı modeli Autodesk Mechanical Desktop programında hazırlanmış
olup, Ansys analiz programı içerisine SAT formatında transfer edilmiştir.
Ansys içerisinde sonlu elemanlar modeli hazırlanmaya başlamadan önce model
üzerinde değişiklik yapmak; sonlu
elemanlar modelinin hazırlanması ve çözüm zamanının azaltılması açısından
faydalı olacaktır. Parçanın şekli itibariyle kabuk teorisine uygundur. Bu yüzden
öncelikle katı olarak gelen modelin dış yüzeyleri kullanılarak kabuk
modeli elde edilmiştir.
Parçaların sonlu
elemanlar modeli Şekil 1.de görülmektedir.
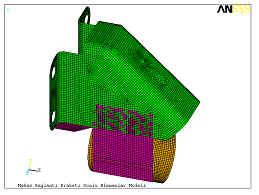
Şekil 1. Makas Bağlantı
Braketi Sonlu Elemanlar Modeli
5. Malzeme Özellikleri
Bu analizlerde
kullanılan parçaların saç kalınlıkları ve malzeme özellikleri Çizelge 1
de görülmektedir. Bu parçanın optimizasyon analizleri yapılacağından
braketi oluşturan saç kalınlıklarının tasarım değişkeni olarak tanımlanması
gerekmektedir. Ayrıca, bu tasarım değişkenleri analiz sırasında kullanılacağından
birer parametreye atanması gerekmektedir. Burada,
Çizelge 1. Saç Kalınlıkları
ve Malzeme Özellikleri
|
|
Braket |
Silindir |
Destek Parçaları |
|
Elastisite Modülü |
210.109 Pa |
210.109 Pa |
210.109 Pa |
|
Poisson Oranı |
0.3 |
0.3 |
0.3 |
|
Yoğunluk |
7860 Kg/m³ |
7860 Kg/m³ |
7860 Kg/m³ |
|
Akma Mukavemeti |
240 MPa |
240 Mpa |
240 Mpa |
|
Saç Kalınlığı |
6 mm |
7 mm |
5 mm |
t1 = 5
mm (Destek parçası saç kalınlığı)
t2 = 6
mm (Braket saç kalınlığı)
t3 = 7
mm (Silindir saç kalınlığı)
6. Sınır Şartları
Ana makas bağlantı
braketi, üzerinde bulunan dört adet delik kullanılarak cıvatalar vasıtasıyla
şasiye bağlanmaktadır. Bu analizde şasi üzerinde oluşacak gerilme dağılımı
bizim için önemli olmadığından şasi modellenmemiştir.
Silindirin iç yüzeyinden
yukarı doğru 600 Kg.lık bir yük, yana doğru 300 Kglık bir başka yük
ile birlikte 12 Kg.mlık bir tork yapı üzerine aynı anda uygulanmaktadır.
Sınır şartları ve yükleme durumları Şekil 2de görülmektedir.
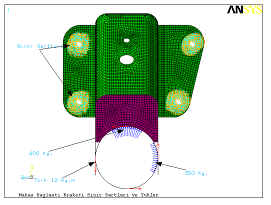
Şekil 2. Makas Bağlantı
Braketi Sınır Şartları ve Yükleme Durumları
7. Analiz Sonuçları
Yukarıdaki yükleme
durumlarına ve sınır şartlarına bağlı olarak çözdürülen model üzerindeki
gerilme dağılımı Şekil 3. ve Şekil 4te görülmektedir. Maksimum
gerilme 200 Mpadır.

Şekil 3. Makas Bağlantı
Braketi Eşdeğer Gerilme Dağılımı
Maksimum gerilme Şekil
3 te görüldüğü gibi destek elemanın yan braketle birleştiği noktada görülmektedir.
Optimizasyon
analizlerinde maksimum gerilme değeri durum değişkeni olarak tanımlanmaktadır.
Durum değişkenler tasarım değişkenleri ile değiştiğinden bu değerinden
parametrik olarak tanımlanması gerekmektedir. gerilme değerinin parametrik
olarak tanımlanması Ansys programı içerinde paramatreler bölümden gerçekleşmektedir.
Bunun sebebi maksimum gerilme değerinin yerinin değişken olmasıdır.
Hedef fonksiyonumuz
minimum hacim olduğundan toplam hacim değerinin de parametre olarak atanması
gerekmektedir.

Şekil 4. Makas Bağlantı
Braketi Eşdeğer Gerilme Dağılımı
8. Optimizasyon Analizleri
Ana makas bağlantı
braketinin statik analizi sonucu oluşan gerilme dağılımı şekil 4te görülmektedir.
Ana makasa bağlantı braketinin akma mukavemeti ve saç kalınlıkları Çizelge
2de görülmektedir.
Çizelge 2. Ana makasa
bağlantı braketi saç kalınlığı ve akma mukavemeti
|
|
Braket |
Silindir |
Destek Parçaları |
|
Akma Mukavemeti |
240 MPa |
240 Mpa |
240 Mpa |
|
Saç Kalınlığı |
6 mm |
7 mm |
5 mm |
- Tasarım değişkenleri
Bu parçanın
optimizasyon analizinde tasarım değişkenleri olarak sadece saç kalınlıkları
alınmıştır. Yapılacak analiz sonucunda optimum saç kalınlıklarının
bulunması istenmektedir. Bu yüzden kullanılan tasarım değişkenleri;
t1=5 mm t2=6 mm t3=7
mm
Bu değişkenler için
kullanılan tasarım sınırlamaları ise;
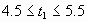
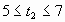
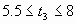
olarak belirlenmiştir.
- Durum değişkenleri
Ana makasa bağlantı
braketinin akma mukavemeti 240 Mpa olduğundan istenen maksimum gerilme 240
Mpa olarak belirleyebiliriz. Parça üzerinde uygulanan sınır şartları
nedeniyle sınır şartlarının uygulandığı noktalarda bölgesel yüksek
gerilmeler çıkmaktadır. Bu yüksek gerilmeler gerçekte yoktur sadece parçanın
bu noktalardan tutulması sebebiyle oluşan
gerilmelerdir. Optimizasyon analizleri sırasında bu yüksek gerilme değerleri
dikkate alınmayacaktır.
- Hedef fonksiyonu
Hedef fonksiyonu
gerilme değerinin verilen sınırlar içinde kalması ile minimum saç kalınlığı
bulunması istenmektedir. Bunun için minimum saç kalınlığı minimum
hacim demektir. Bu durumda hedef fonksiyonu minimum hacimdir.
- Optimizasyon metodu
Bu analizde Alt
problem yaklaşımı metodu kullanılmıştır. Bu metot hakkında ayrıntılı
bilgiler bölüm 3 ve bölüm 5te verilmiştir.
Alt problem yaklaşımında
kullanılan maksimum iterasyon sayısı 30 olarak alınmıştır.
- Analiz sonuçları
Yapılan
optimizasyon analizi sonucu elde edilen sonuçları Çizelge 3. te
verilmiştir.
Çizelge 3 Alt
problem yaklaşımı tasarım değişkenleri setleri
| |
SET 1 |
SET 2 |
SET 3 |
|
Gerilme |
0.27322E+09 |
0.26964E+09 |
0.26563E+09 |
|
t1 |
0.49864E-02 |
0.53472E-02 |
0.51924E-02 |
|
t2 |
0.59760E-02 |
0.59144E-02 |
0.60751E-02 |
|
t2 |
0.91058E-02 |
0.70820E-02 |
0.74269E-02 |
|
Hacim |
0.32919E-03 |
0.30832E-03 |
0.31455E-03 |
| |
SET 4 |
SET 5 |
SET 6 |
|
Gerilme |
0.31834E+09 |
0.25338E+09 |
0.24733E+09 |
|
t1 |
0.53478E-02 |
0.48203E-02 |
0.52282E-02 |
|
t2 |
0.50067E-02 |
0.65855E-02 |
0.65083E-02 |
|
t2 |
0.72036E-02 |
0.73732E-02 |
0.67073E-02 |
|
Hacim |
0.28619E-03 |
0.32227E-03 |
0.31773E-03 |
| |
SET 7 |
SET 8 |
SET 9 |
|
Gerilme |
0.24545E+09 |
0.24083E+09 |
0.23964E+09 |
|
t1 |
0.52381E-02 |
0.52511E-02 |
0.51313E-02 |
|
t2 |
0.65486E-02 |
0.66607E-02 |
0.67659E-02 |
|
t2 |
0.66812E-02 |
0.65597E-02 |
0.65189E-02 |
|
Hacim |
0.31860E-03 |
0.32025E-03 |
0.32091E-03 |
- Sonuçların yorumlanması
8 iterasyon sonunda en
iyi tasarım değişkenlerine ulaşılmış ve iterasyon durdurulmuştur. Çizelge
4te bu parçanın optimizasyonu işleminde bulunan en iyi tasarım değişken
seti görülmektedir.
Çizelge 4. En iyi tasarım
değişkeni tasarım seti
| |
SET 8 |
|
Gerilme |
0.24083E+09 |
|
t1 |
0.52511E-02 |
|
t2 |
0.66607E-02 |
|
t2 |
0.65597E-02 |
|
Hacim |
0.32025E-03 |
Ana makas bağlantı
breketinin ilk haldeki durumu gerilme bakımından mukavemetsiz olduğu görülmektedir.
Bu durum için yapılan optimizasyon analizinde gerilme değerinin akma
mukavemeti değerini altına düşmesi amaçlanmaktadır. Bu amaça ulaşmak için
kriterimiz minimum hacimdir.
Tasarım değişkenlerinin
başlangıç değerleri;
t1=5 mm t2=6 mm t3=7
mm
analiz sonuçlarında
oluşan yeni tasarım değişkenleri ise;
t1=5.2515 mm t2= 66 mm t3=
5597 mm
olarak bulunur. Burada;
braketin ve silindirin saç/et kalınlıkları artmasına rağmen destek parçasının
gerilme değeri düşmektedir.
Şekil 7 ve Şekil 8 de
Hacim ve Gerilme değişimi görülmektedir. Bu iki şekil incelendiğinde Hacim
miktarının minimum olduğu dördüncü iterasyonda gerilme değeri maksimum
olup akma mukavemetinin üzerindedir. İstenen şartların hepsini aynı anda sağlayamadığından
dolayı iterasyonlara devam edilmiştir.
Gerilmenin akma
mukavemetinin altına düştüğü sekizinci iterasyon verilen kısıtlamaların
hepsini aynı anda sağladığından analiz sonuçlandırılmıştır.
Sonuç olarak; gerilme
bakımından akma mukavemetinin altında maksimum gerilme değerine sahip,
minimum hacimli tasarım değişkenleri bulunmuştur.
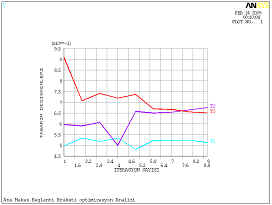
Şekil 5. Tasarım değişkenlerinin
değişimi
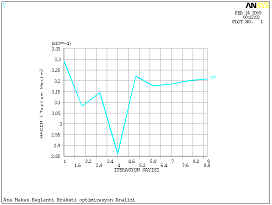
Şekil 6 Hacim değişimi
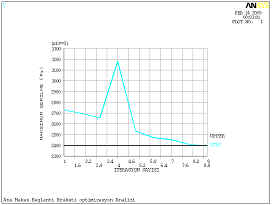
Şekil 7. Gerilme değişimi
|
