|
4.3.2 Eleman Seçimi
Sonlu elemanlar ile modelleme aşamasında,
"eleman tipi (çubuk, kabuk. v.s). eleman şekli (dörtgen, üçgen) ve
eleman sayısı ne olmalı?", "ara nodlu elemanlara ihtiyaç
var mı?" gibi bir takım soruların cevaplanması
gerekmektedir. Bu soruların cevabı ancak analiz edilen yapının
ve seçilen eleman tiplerinin davranışı hakkında bilgi
sahibi olunduktan sonra cevaplanabilir. Örneğin, gerilme
analizinde yapının bir bölgesindeki gerilme durumunu en iyi yansıtan
eleman tipi o bölge için seçilmelidir. Aşağıda bazı
eleman tipleri ve bunların kullanılabileceği mühendislik problem
tipleri haklarında bilgi verilmektedir.
4.3.2.1 3D Kiriş Elemanı
3D Kiriş elemanı genel amaçlı bir sonlu
eleman tipi olup 3 boyutlu işlemi yapabilme kapasitesine sahiptir. Bu
eleman tipi aynı zamanda uzay kiriş elemanı olarak da adlandırılmaktadır.
Eleman uzayda iki adet nod ile tarif edilmektedir. Üçüncü bir nod ise
serbestlik derecesine haiz olmayan ve eleman koordinat sistemini tarif etmek
amacıyla kullanılmaktadır. Elemanın iki ucunu tespit eden
iki adet nod için 12 adet serbestlik derecesi mevcuttur. Her bir nod 3 adet öteleme
ve 3 adet dönme serbestliğine sahi ptir.
Eleman herhangi doğrultuda gelen kuvvet ve herhangi bir eksen etrafında
dönme zorlamasına direnç gösterecek kapasiteye sahiptir. Elemanı
tarif etmek için nodların koordinatına, elastisite modülüne (E),
kayma modülüne (G), kesit alanına, kesit atalet momenti
değerlerine, burulma sabitine (J) ve kiriş eksenine dik doğrultudaki
deformasyon faktörlerine ihtiyaç vardır
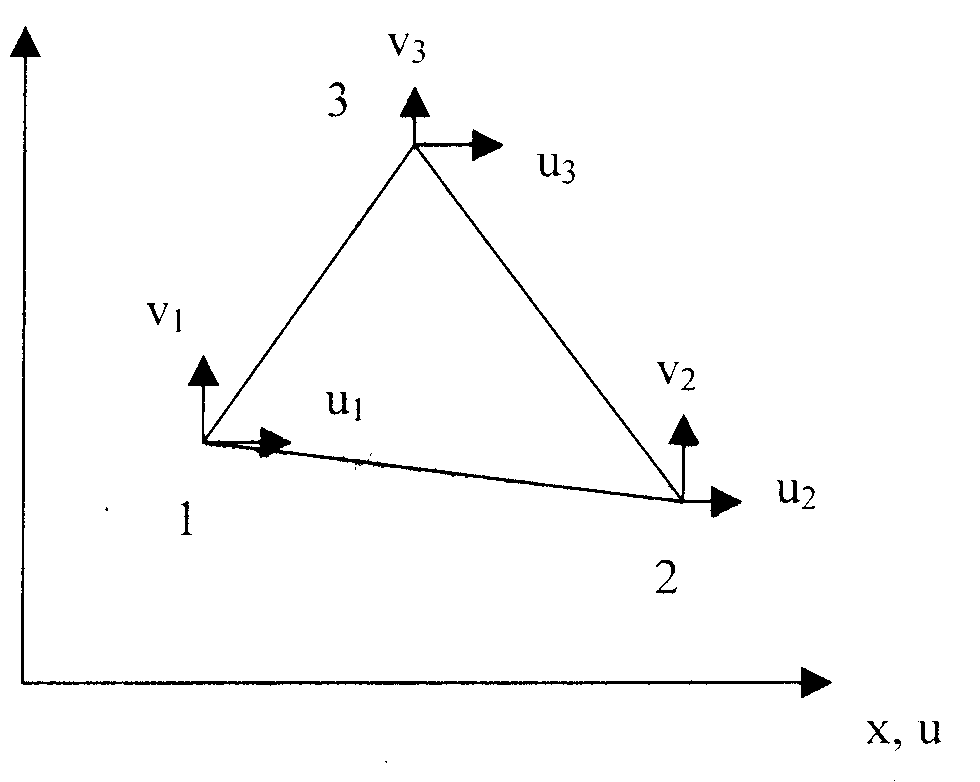
4.3.2.2 Sabit Gerilmeli Üçgen Eleman (SGU)
SGU elemanı sabit kalınlığı olan,
üç nod noktasını birleştiren ve toplam altı serbestlik
derecesi ile tarif edilen bir elemandır (Şekil xxx). Eleman deplasman
alanı aşağıdaki gibi tarif edilmektedir.
u = a1 + a2x + a3y (4.1)
v = a4 + a5 + a7y (4.2)
 Yukarıdaki deplasman bağıntılarından görüldüğü
gibi deplasman alanı eleman içinde ve kenarlar boyunca lineerdir. Eleman sınırları
içinde ise gerilme değerleri sabittir. Birbirine bağlı elemanlar
arasında deplasman uyumluluğu (compatibility), bağlı iki nod
noktası arasındaki lineer kenar deformasyon karakteristiği dolayısıyla
sağlanmaktadır. Yapının
bütün olarak kuvvet dengesi ise nod noktalarında sağlanır.
Yukarıdaki deplasman bağıntılarından görüldüğü
gibi deplasman alanı eleman içinde ve kenarlar boyunca lineerdir. Eleman sınırları
içinde ise gerilme değerleri sabittir. Birbirine bağlı elemanlar
arasında deplasman uyumluluğu (compatibility), bağlı iki nod
noktası arasındaki lineer kenar deformasyon karakteristiği dolayısıyla
sağlanmaktadır. Yapının
bütün olarak kuvvet dengesi ise nod noktalarında sağlanır.
Şekil xxx Sabit Gerilmeli Üçgen Eleman
SGU elemanı sonlu eleman modellerinde küçük gerilme
gradyeni karakteristiğine sahip bölgelerde iyi sonuç verecektir. Diğer
durumlarda SGU elemanının kullanılması iyi sonuç
vermeyecektir. Örneğin sadece eğilmeye maruz bir yapıyı SGU
elemanlarıyla modellemek gerçek problem ile uyumsuz sonuçlar verecektir.
SGU elemanlarının bu olumsuzlukları, daha sık bir eleman ağ
yapısıyla kısmen giderilebilir .
4.3.2.3 Lineer Gerilmeli Üçgen Eleman(LGU)
LGU elemanları SGU tip elemanların aksine, köşe
noktalarına ilaveten kenar orta noktalarında birer adet daha nod
noktasına sahiptir. Böylece her bir LGU elemanı 6 adet nod noktasına
ve toplam olarak 12 nod serbestlik derecesine sahiptir. Eleman deplasman alanı
ise aşağıdaki gibi tarif edilmektedir.
u = a1 + a2 x + a3 y + a4 x2
+ a5 xy + a6 y2 (4.3)
v = a7 + a8 x + a9 y + a10 x2
+ a11 y + a12 y2 (4.4)
SGU elemanının aksine
gerilme büyüklüğü LGU elemanı içerisinde x ve y koordinatları
ile lineer olarak değişmektedir. Sadece eğilmeye maruz yapılar
için LGU elemanlarıyla yapılan modellemelerde, deplasman ve gerilme
alanları için çok iyi yaklaşımlar elde edilecekdir.
4.3.2.4 Çifte Lineer Dörtgen Eleman
2 Boyutlu problemler için diğer bir tip eleman, çifte
lineer dörtgen elemanlardır. Eleman köşelerinde dört adet nod yer
almaktadır ve eleman sekiz nodal serbestlik derecesine sahiptir. Diğer
yandan 8 nodlu eleman tipi için ise kenarların orta noktalarında dört
adet nod vardır. Dört nodlu eleman için deplasman alanı aşağıdaki
bağıntılarda verilmiştir.
u = a1 + a2 x + a3 y + a4xy (4.5)
v = a5 + a6 x + a7 y + a8xy (4.6)
Burada elemanın çifte lineer diye
isimlendirilmesi u ve v deplasman bağıntılarının iki
lineer polinomun çarpımından oluşmasından dolayıdır.
Şekil xxx Dört Nodlu Çifte Lineer Dörtgen
Eleman
Elemanın en önemli özelliği sx
değeri x- koordinatından bağımsızdır. Bu eleman
tipi, örneğin ucundan yüklü konsol kirişlerin modellenmesinde uygun
sonuç vermeyecektir
4.3.2.5 Kabuk Elemanlar
Bir genel kabuk eleman membran ve eğilme etkisini aynı
anda temsil edebilmelidir. Örneğin dört nodlu basit bir dörtgen eleman
tarif edilebilir. Elemanı tarif eden tüm nodlar aynı düzlem üzerinde
olmayabilir. Bu da elemanda çarpılmaya neden olur. Elemanın çarpılması
performansını olumsuz yönde etkiler. Ticari paket programlarda küçük
miktarlarda çarpılmaya müsaade edilmektedir. Bu dört
nodlu elemanın en büyük avantajı formülasyonunun basit olmasıdır.
Genellikle az sayıda daha karışık bir eleman tipi kullanılması
yerine, daha fazla sayıda basit bir eleman tipi kullanılması
tavsiye edilmektedir. Dört kabuk elemanın en büyük dezavantajı
düzgün eğrisel yüzeylerin düzlem elemanlarla veya az miktarda çarpılmış
şekle sahip olan elemanla temsil edilmesidir. Kabuk teorisine dayanarak
elde edilen eğrisel yüzeyli elemanlar düzlemsel elemanların yaratmış
olduğu problemleri ortadan kaldırmaktadır. Fakat diğer
yandan beraberinde başka zorlukları getirmektedir. Eğrisel elemanı
tarif etmek için çok daha fazla geometrik bilgiye ihtiyacımız
olmaktadır. Elemanın formülasyonu ise düzlemsel elemanlara nazaran
çok daha zordur.
.
4.3.2.5.1 Dört Nodlu ve Dört Kenarlı
Elastik Kabuk Eleman
Çoğu ticari programda yer alan bu eleman tipi eğilme
ve membrane yüklerini taşıyabilme özelliğine sahiptir. Eleman düzlemi
içinde ve düzlemine dik doğrultudaki yüklemelere müsaade eder. Her nod,
üç tanesi x, y, z- doğrultusunda öteleme ve üç tanesi de bu eksenler
etrafında dönme serbestliği olmak üzere altı adet serbestlik
derecesine sahiptir ( Şekil xxx). Eleman dört nod ile tarif edilmekte ve
değişken kalınlığa müsaade edilebilmektedir. Değişken
kalınlıklı elemanlar iç in
kalınlık eleman içerisinde düzgün olarak değişmelidir. Bu
eleman tipi plakların olduğu kadar düzgün eğrisel yüzeylerin
modellenmesinde de kullanılmaktadır. Eğrisel yüzeylerde iyi bir
yaklaşım elde edebilmek için fazla sayıda bu elemandan kullanılmalıdır.
Formülasyonunun basit olması nedeniyle diğer tip elemanlara göre
daha avantajlıdır.
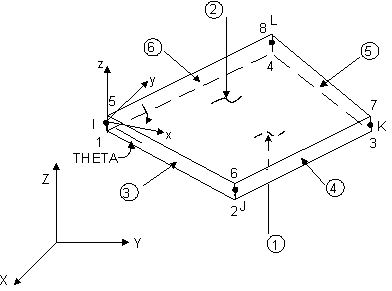
Şekil xxx Dört
nodlu ve dört kenarlı elastik eleman (x,y eksenleri eleman düzlemi içindedir).
4.3.3 Yükler
Tekil yükler mutlaka nod noktalarına uygulanmalıdır.
Bu nedenle ağ yapısı tekil yüklerin nodal noktalara uygulanmasını
sağlayacak şekilde yapılandırılmalıdır.
Klasik lineer teoriye göre bir noktaya tekil yük uygulandığı
zaman, o noktada;
- kiriş için sonlu bir deplasman ve gerilme değeri oluşur,
levha için sonlu deplasman, sonsuz gerilme değeri
oluşur,
iki veya üç boyutlu geometrik cisim için ise sonsuz deplasman ve
gerilme değeri oluşur.
Diğer yandan bir tekil yük malzemede o bölgede akmaya
neden olacaktır. Lineer teori ise akmayı modellemez. Sonuç olarak
tekil yükler küçük alanlar üzerine dağıtılmış yüksek
yoğunluklu yayıl yükler olarak modellenebilir. Eğer tekil yük
bir nod noktasına uygulanırsa sonsuz deplasman ve gerilme değerleri
hesaplanmaz.
Bir tekil moment sadece öteleme serbestlik derecesine sahip
bir noda uygulanamaz. Bu durumda tekil momentler eşlenik kuvvetler olarak
temsil edilirler. Diğer yandan yayılı yükler nod noktalarına
tekil yükler olarak uygulanırlar.
4.3.4 Sınır Koşulları
Sınır koşulları yapıların
mekaniğinde mesnet şartları olarak da isimlendirilmektedir. Sonlu
eleman modellemelerinde sınır koşulları (mesnet şartları)
sık sık yanlış veya eksik olarak tanımlanmaktadır.
Modellemede sınır koşullarına gerekli özen daima gösterilmelidir.
Her ne kadar yapılan hata küçük gibi görülse de ,
sonuçlar üzerindeki etkisi oldukça büyük olacaktır. Örneğin
Şekil xxx de görülen ve iki ucu basit mesnetlenmiş kirişin
sonlu elemanlar modelinde, elemanlar tarafsız ekseninden geçen çizgi üzerinde
yer alırlar. Kiriş parçasının uçlarının yatay doğrultudaki
hareketi sınırlandığı için, kiriş bu doğrultuda
zorlanmaya maruz kalacaktır. Bu nedenle kirişin sonlu eleman modelinin
uçları düşey bağlantılarla A ve B noktalarına bağlanır.
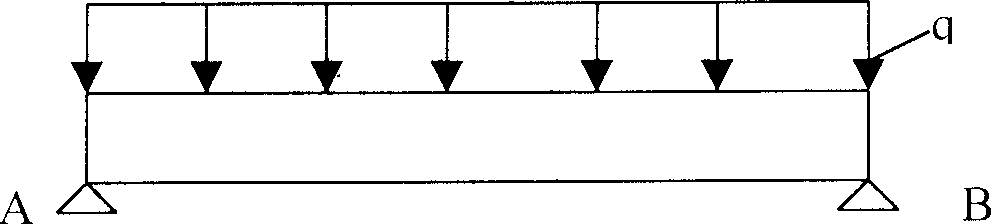
Şekil xxx İki
ucu basit mesnetli kiriş
Sonlu elemanlar modelinde aktif olmayan
serbestlik dereceleri çözüm işleminden önce sınırlandırılmalıdır.
Bu sınırlandırılması gereken serbestlik derecesi
modelin sınırda veya başka bir bölgesinde olabilir. Örneğin
düzlem elemanlar nodlarda düzlem içinde iki doğrultudaki ötelemeye karşı
direnç gösterirler. Fakat genel amaçlı
bir sonlu elemanlar programı her bir noda üçü öteleme ve diğer
üçü de dönme olmak üzere altı serbestlik derecesi atayacaktır.
Rijidlik matrisinde tekillikleri önlemek amacıyla düzlem elemanlar için
her noddaki üç dönme serbestliği ve
eleman düzlemine dik doğrultudaki öteleme serbestliği kısıtlanmalıdır.
Çünkü seçilen eleman tipi bu serbestlik dereceleri için direnç gösteremeyeceğinden,
rijidlik matrisinde tekillikler oluşacak, bu da denklemlerin çözümünü
zorlaştıracak veya imkansız
hale getirecektir. Doğru bir modelleme için düzlem elemanların her
bir nodu için üç serbestlik derecesi atanır. Sınır koşulları
için ise yine sınırda yer alan nodlar için bu serbestlik
derecelerinden bazılarının kısıtlanması
gerekebilir.
Bazı durumlarda gerçek problem için sınır koşulları
net olarak anlaşılır olmayabilir. Böyle durumlar için çözümün
üst ve alt sınırlarını iki ayrı analizle saptamak fıziksel
olarak daha anlamlı olabilir. Örneğin iki ucundan mesnetlenmiş
üniform yüklü bir kirişin uçları
dönmeye belli olmayan bir dereceye kadar kısıtlanmış
olabilir. Böyle bir durum için kirişin uçları bir çözüm için
basit mesnetli olarak kabul edilir, diğer bir analiz içinse tamamıyla
tespit edilmiş olarak kabul edilerek problem çözülür: İki analizden
elde edilen değerler aslında gerçek problem için alt ve üst sınırları
göstermektedir.
4.3.5 Ayrıklaştırma ve Dikkat Edilmesi Gerekli Hususlar
Bir problemin sonlu elemanlar metoduyla çözümü için kaç
adet eleman gereklidir? Böyle bir soruya cevap aramak için
aynı problemi iki farklı modelle ayrı ayrı analiz edelim.
İkinci analizde daha fazla sayıda eleman ile daha sık bir ağ
kullandığımızı farz edelim. İkinci sonlu eleman
modeli daha küçük bir ayrıklaştırma hatası verecektir.
Ayrıca gerçek fıziksel objenin
geometrisi daha iyi modellenmiş olacaktır. Eğer iki analiz
neticesinde bulduğumuz sonuçlar arasında önemli bir fark yoksa, sonuçların
yakınsamış olduğunu kabul edebiliriz.
Yazılımlarda genelde bir takım hatalar
bulunabilir. Sonlu eleman paket programları oldukça büyük yazılımlar
olup, devamlı düzeltmeler yapılmaktadır. Elde edilen hatalı
sonuçlar için programı suçlamak kolay bir yol olmasına rağmen,
hatalı sonuçlara genelde yanlış modellemeler neden olmaktadır.
Doğru modelleme yapabilmek için ayrıklaştırma
esnasında bir takım hususlara dikkat edilmesi gerekmektedir. Bu
hususlar aşağıda sıralanmaya çalışılmıştır.
- Sonlu elemanlar grid ağının mümkün olduğu kadar üniform
olmasına dikkat edilmelidir. Fakat yüklemede ve yapının
davranışında hızlı değişimlerin görüldüğü
bölgelerde daha sık bir ağ yapısı için üniformluğun
bozulmasına müsaade edilebilir.
- Dört kenarlı elemanların üçgen elemana göre bir çok avantajı
olması nedeniyle, dört kenarlı elemanlar daima üçgen elemanlara
tercih edilmelidir. Fakat geometrinin ve/veya yüklemenin üçgen eleman
gerektirdiği durumlarda bu kural bozulabilir.
- Deplasman analizi için gerilme analizinde kullanıldığı
kadar sık ağ yapısına gerek yoktur.
- Geometride veya malzemede non-lineerliliği hesaba katan analizler için
lineer analizlere kıyasla daha sık bir ağ yapısına
ihtiyaç vardır.
- Titreşim nodlarının hesabı doğal frekansların
hesabına kıyasla daha sık ağ yapısı
gerektirmektedir.
- Nodların numaralandırılması mümkün olduğu kadar
büyük deplasman bölgelerinden küçük deplasman bölgelerine doğru
yapılmalıdır. Fakat genelde sonlu eleman paket programlarında
sonuçlar numaralandırmadan etkilenmezler
- Eğrisel yüzeylerin düzlemsel elemanlar ile tarif edilmesi durumunda
yüzey normali etrafındaki dönme serbestliği kaldırılmalıdır.
Aksi taktirde kötü koşullu bir matrisle uğraşılması
gerekecektir.
- Elemanların kenar uzunluk oranları (aspect ratio) eleman tipleri
arasında değişiklik gösterse de, uzunluk oranı
deplasman hesapları için 10'un altında,gerilme hesapları için
ise 5'in altında kalmalıdır.
- Yüksek mertebeden elemanlar için ara nodların dağılımı
mümkün olduğu kadar üniform olmalıdır.
- Sonlu eleman hesaplarının ilk kontrolü için yüklerin,
kuvvetlerin ve reaksiyonların dengesinin kontrol edilmesi tavsiye
edilmektedir.
- Eğer analiz edilen yapı ve yükleme simetrik ise, hesaplamalarda
bu avantaj kullanılmalıdır. Yani analiz için yapının
yarısı veya dörtte biri modelleme için kullanılabilir.
Fakat burkulma ve özdeğer problemlerinde dikkatli olunması
gerekir. Çünkü anti-simetrik nodlar bu problemler için önemli olabilir.
- Yüksek frekanslı tepkisel değerlerin önemli olmadığı
dinamik analizler için. statik analizde kullanılana benzer bir ağ
yapısı yeterli olacaktır.
- Transient dinamik analizlerde eleman boyu, zaman adımı,
integrasyon metodıı ve pulse süresi uyumlu olmalıdır.
- Yüksek uzunluk oranlı dörtgen elemanlar, büyük açılı
üçgen eleman gibi elemanlardan mümkün olduğu kadar sakınılması
gerekmektedir.
- Yakınsaklık analizinde orijinal mesh kullanılarak ağ sıkılaştırılmalıdır.
Eğer farklı bir mesh kullanılırsa yakınsaklık
analizine tekrar başlamak gerekecektir.
- Yüksek ve düşük mertebeden elemanların birbirine bağlanması
gerilmelerde düzensizliklere neden olacaktır.
- Eleman boyutlarında hızlı değişiklikler mümkün
olduğu kadar minimize edilmelidir
- Anisotropik malzemeler için Poisson oranı açıkça tanımlanmalıdır.
Ayrıca
n,
E ve G değerlerinin teorik limitlerinin aşılıp aşılmadığı
kontrol edilmelidir.
- Kompleks yapıların sonlu elemanlar metoduyla analizinde, tüm
yapı göreceli olarak kaba bir ağ yapısıyla analiz
edilir. Bu analiz sonuçları yapı içinde detaylı bilgi
sahibi olmak istediğimiz bölge için sınır koşulu
olarak kullanılarak, bu bölge daha sıkı bir ağ yapısı
ile analiz edilebilir.
4.3.6 Sonlu Eleman Program Kullanıcısının
Sorumlulukları
Günümüzde ticari sonlu eleman paket programları son
derece yaygınlaşmıştır. Tecrübesiz bir kullanıcı
bile bir takım sonuçlar üretip, son derece cazip grafıkler hazırlayabilir.
Örneğin bir gerilme analizi için sonlu eleman modeli iyide olsa, kötüde
olsa ehliyetsiz bir kullanıcı bile kolaylıkla gerilme konturları
üretebilir. Kötü bir ağ yapısı, kötü seçilmiş eleman
tipleri, doğru olmayan yük leme şekliyle
yaratılan modeller bile dikkatsizce yapılan bir kontrolde gözden kaçabilecek
uygunlukta sonuçlar verebilir.
Ehliyetli bir kullanıcı ancak mevcut problemin fiziğini
anladıktan sonra uygun bir modellemeye gidebilir ve sonuçları
yorumlayabilir. Kullanıcı aynı zamanda yarattığı
modelin yükleme altında nasıl davranacağını öngörebilmelidir.
Gerilme analizinde uzmanlaşmış olmak, örneğin manyetik alan
problemlerinin çözümünde yeterli olmak anlamına gelmemektedir. Elde
edilen çözümlerdeki yanlışlıklar yazılımdaki
hatadan kaynaklansa bile sonuçların sorumluluğu programcıya değil,
kullanıcıya aittir.
4.4 Sonlu Elemanlar Analizlerleri
4.4.1 Statik Analiz
4.4.1.1 Giriş
Statik analizde zaman bağımsız bir değişken
olarak göz önüne alınmaz. Deformasyonların sabit ve yavaşça
değiştiği kabul edilir. Bazı problemlerde titreşim
frekansı çok düşük olabilmektedir (en düşük doğal
frekansın 1/3'ünden daha küçük). Bu durumlarda problem "quasi-statik"
olarak düşünülebilir. Yani atalet kuvvetleri hesaplanarak, bunlar
sanki birer statik yükmüş gibi yapıya
uygulanarak, yapı statik olarak analiz edilebilir [Engin, A. ve ark.2000].
Bir statik analiz için aşağıdaki adımların
yerine getirilmesi gerekmektedir:
1. Sonlu elemanlar modelini hazırla.
- yapıyı sonlu elemanlara bölerek ayrıklaştır.
- yapının nasıl yüklendiğini tanımla
- yapının nasıl desteklendiğini tanımla
2. Hesaplamaları gerçekleştir. Program sırasıyla
aşağıdaki adımları gerçekleştirir.
Rijitlik matrisi [K] her bir eleman için
hesaplanır.
Elemanlar birbirleriyle birleştirilerek, tüm
sistem için global rijitlik [K] elde edilir.
Yükler global yük vektöründe, [R],
yerleştirilir.
Mesnet koşulları uygulanır.
Global denklem takımı [K] . [D]= [R],
bilinmeyen [D] değerleri için çözülür.
Yapı problemlerinde [D] matrisi nodal
deplasman değerlerini temsil etmektedir.
Sonuçları ([D]
matrisini) kullanarak, örneğin gerilme değerlerini hesaplayınız.
4.4.1.2 Rijitlik Matrisinin Oluşumu
Genel olarak rijitlik matrisi [K]
bir eleman için aşağıdaki şekilde temsil edilebilir.
[K]= ( [B]T [E] [B] dV
Burada [B] şekil değiştirme-deplasman
matrisi, [E] sabitler matrisi olup,
malzeme özelliklerini göstermektedir. dV ise elemanter hacim elemanıdır.
Rijitlik matrisleri eleman tipine bağlı olarak, eleman deplasman alanını
tarif eden şekil (shape functions) fonksiyonları kullanılarak her
tip eleman için ayrı ayrı hesaplanabilirler (örneğin kaynaklar
16-18'e bakınız).
Eleman rijitlik matrisiyle, sistem global rijitlik matrisleri
simetriktir. Bu durum yapıya etkiyen kuvvetler ile deformasyonlar arasında
lineer ilişki olduğu sürece geçerlidir. Rijitlik matrislerinde
diyagonal terimler daima pozitiftir. Diğer yandan bir yapı hiç
mesnetlenmemiş veya uygun şekilde mesnetlenmemişse, rijidlik
matrisinde tekillikler oluşur. Bıı durumda program [K]
. [D] _ [R] denklemini nodal serbestlik
dereceleri için çözemeyecektir. Matristeki tekillikleri önleyebilmek amacıyla
tüm rijid cisim hareket serbestlikleri uygun şekilde engellenmelidir. Bu
rijid hareket serbestlikleri yapı içerisinde deformasyon ve dolayısıyla
gerilme yaratmayan hareket şekilleridir.
Her bir nod noktasına genel amaçlı bir sonlu
eleman programı altı serbestlik derecesi atayacaktır. Bunlar üç
adet öteleme ve üç adette dönme serbestliğidir. Eğer bu global
serbestlik derecelerinden biri bile bu noda bağlı olan elemanların
biri için bile şekil değiştirme oluşturmuyorsa, rijitlik
matrisinde tekillik oluşacaktır. Bu tür serbestlik dereceleri çözümden
önce kısıtlanmalıdır.
4.4.1.3 Yükler
Yükler yapıya değişik şekillerde
uygulanabilir. Bu tek bir noktaya uygulanan kuvvet veya moment olarak veya yüzey
basınç yükü olarak gerçeklenebilir. Diğer bir yükleme şekli
ise cismin kendi ağırlığı dolayısıyla veya
atalet kuvvetlerinin varlığı dolayısıyla oluşan
kuvvetlerdir.
Yayılı yükler sonlu eleman programlarında
"Kinematik Eşdeğer" nodal yüklerle değiştirilirler.
Kinematik eşdeğer nodal yükler toplamda orijinal yüke eşit
olup, herhangi bir noktaya göre orijinal yüklemeyle aynı moment değerini
vermektedir. Kinematik eşdeğer olmayan nodal yüklemeler
ise genelde "lumped" yükleme olarak adlandırılır ve
genelde dönme serbestliğine sahip elemanlar için tercih edilmektedir.
4.4.2 Titreşim Ve Dinamik Analiz
4.4.2.1. Giriş
Bir yapı üzerine yapılan yükleme altında
hareket edecektir. Eğer yükleme bir frekansa bağlı olarak değişiyor
ve bu frekansta yapının doğal frekansının 1/3'den daha
düşük ise problem statik problem olarak sınıflandırılabilir.
Diğer yandan yükleme yüksek frekanslı veya rastgele olarak değişiyorsa
veya yük aniden uygulanıyorsa, problem
için dinamik analiz gerekmektedir. Dinamik analizde de statik analizde olduğu
gibi rijitlik matrisi kullanılmakta, fakat bir kütle ve bir sönüm
matrisine de analiz için gerek duyulmaktadır.
4.4.2.2 Temel Titreşim Denklemleri
En basit bir titreşim sistemi tek serbestlik dereceli
bir yay-kütle sistemidir. Burada kütlenin hareketi yatay doğrultuda tek
bir koordinatla tamamıyla tarif edilmiş olmaktadır. (Şekil
xxx). Sistemin hareketi Newton'un 2. hareket kanunu ile tarif
edilmektedir.
Newton'un ikinci kanununu uygularsak f = ma, sistemin hareket
denklemi sönümsüz titreşim için aşağıdaki şekli alır.
r ku = mü veya ku + mü = r (4.7)
Burada r dışardan etkiyen ve zamana bağlı
olanak değişen yüklemeyi göstermektedir. Eğer titreşim
sistemi için sönüm kuvvetlerini de hesaba katarsak (4.7) deki denklem aşağıdaki
formda yazılmalıdır.
r ku cü = mü veya ku + cü + mü = r (4.8)
Burada m kütleyi, c ise sönüm katsayısını
göstermektedir.
Eğer bir sonlu eleman modellemesinde olduğu gibi çok sayıda
serbestlik derecesi ile ilgileniyorsak (4.8) deki denklemi matris formunda
yazmalıyız
[K].[D] + [C].[D] + [M].[D] = [R] (4.9)
Bu denklemde [K] rijitlik matrisini, [C] sönüm matrisini, [M]
kütle matrisini ve [R] kuvvet vektörünü temsil etmektedir. Bir
dinamik analizde bilinmeyen [D] deplasman vektörünün, [ D ]
hız vektörünün ve [ D ] ivme
vektörünün hesaplanması istenmektedir.
4.4.2.3 Matris İndirgeme
Dinamik analizde tüm matris sisteminin çözümü yerine çok
daha az sayıda serbestlik derecesi kullanılarak, yani daha küçük
bir matrisle çözüm yapılabilir. Biz bu işleme matrisin indirgenmesi
işlemi diyoruz. Bu şekilde dinamik analizler daha az bilgisayar
kapasitesi ile gerçeklenebilir. Burada matriste kullanılacak aktif
serbestlik derecelerinin seçimi özel bir önem kazanmaktadır. Bu
serbestlik dereceleri genelde büyük deplasmanlı nodlardan seçilmesi
uygun olacaktır. Çoğu ticari sonlu elema n
programlarında bu serbestlik otomatik olarak seçilebilmekte ve "master"
serbestlik dereceleri otomatik olarak isimlendirilmektedir. En yaygın
olarak kullanılan indirgeme metodu Guyan metodudur. Master serbestlik
dereceleri için aşağıdaki önerilere dikkat edilmelidir.
master serbestlik dereceleri için kütle/rijitlik oranı
büyük olmalıdır.
master serbestlik derecelerinin seçimi yapının
sadece bir bölgesinden değil, tüm bölgelerinden yapılmalıdır.
Aksi halde bazı modlar iyi bazı modlar ise kötü olarak t emsil
edilecektir.
Master'lar beklenen hareket doğrultusunda seçilmelidir.
4.4.2.4 Modelleme
Dinamik yapı analiz, statik analize göre daha fazla çalışma
gerektiren bir analiz türüdür. Yükleme zamanın bir fonksiyonudur.
Dinamik analizde çeşitli metodlar aynı amaca ulaşılabileceği
gibi, aynı model için değişik amaçlar için analizler gerçeklenebilir.
Dinamik analizin diğer bir zorluğu da sonuçların kontrolü için
gerekli adımlardan biri olan yapının davranışını
mevcut şartlar altında kestirmektir (statik analiz
için bu çok daha kolay şekilde yapılabilir). Diğer yandan yapı
statik ve dinamik yükler altında oldukça farklı tepkiler verebilir.
Analizden önce dinamik analizin gerekli olup olmadığına
karar vermek gerekmektedir. Eğer yapı frekansa bağlı bir
kuvvetin altında zorlanıyorsa, zorlayıcı frekans yapının
en düşük doğal frekansıyla karşılaştırılır
ve doğal frekans zorlayıcı frekansın 1/3'ünden daha düşük
ise dinamik analize gerek yoktur, problem statik analiz
İle çözümlenebilir. Genellikle böyle durumlarda
dinamik yüke verilen tepki değeri, dinamik yükün genliğine sahip
statik yükleme altında elde edilecek değerin %10u daha fazladır.
Eğer bir dinamik analiz yapılmasına karar verildiyse bazı
sorulara cevap verilmesi gerekecektir. Bunlar şöyledir; "Analizi n
hedefı nedir ?", "Hangi basitleştirmeleri yapmak mümkündür?",
"Malzeme ve geometrik non-lineerlikler hesaba alınmalı mıdır?",
"Hangi frekans değerleri yüklemede göz önüne alınmalıdır?",
"Hangi frekanslardaki tepkiler yapı için önemlidir?",
"Hangi hesaplama yöntemleri problem için uygundur?".
Dinamik analizlerde ilk adım olarak genelde doğal
frekans değerleri ve bu frekanslara ait şekil değiştirme
modları hesaplanmaktadır. Bu değerler yapının her hangi
bir zorlayıcı kuvvet altındaki davranışını
tespit ederler. Bu modları inceleyerek zorlayıcı kuvvetlerin yapıya
hangi modlarda daha çok enerji verebileceğini ve yapının hangi
noktasındaki tepkiye hangi modun daha büyük katkı yapacağını
görebiliriz.
4.4.2.5 Titreşim Hesabı
Öz değer problemi çözümleri için değişik
çözüm metodları kullanılabilir. Bu metodlar uygulanabilirliği
ve effektifliği açısından farklılıklar göstermektedir.
Metodlar tüm modelin serbestlik derecesinin sayısı ve hesaplanması
istenen mod sayısına göre değişiklikler göstermektedir.
Genellikle çoğu problemlerde az sayıda
modun ve bunlarla ilgili frekans değerlerinin hesaplanması pratik açıdan
yeterlidir. Genellikle, yapının tüm modlarının %10'u
yeterli olmaktadır.
Eğer yapı tamamıyla tespit edilmemişse [K]
rijitlik matrisinde tekillikler oluşacak, bu sebeple de her bir rijid cisim
titreşim modu için sıfır frekans değerleri elde edilmesine
neden olacaktır. Böyle durumlarda programlar öz değerlerde kayma
yaparak, hesaplamaya devam eder. Eğer kütle matrisinin köşegeninde sıfır
değeri varsa, kütle matrisi [M]
de tekillik olacak ve her bir sıfır kütle değeri için sonsuz
frekans değeri bulunacaktır. Bu istenen bir durum değildir.
4.4.3 Termal Analizler
Kartezyen koordinatlardaki ısı transferi denklemi aşağıdaki
şekilde yazılabilir.
 (4.10) (4.10)
Lineer dikdörtgen şekil fonksiyonları sıcaklık
gibi bağımlı değişkenlerin çeşitli varyasyonlarını
ifade ederler nodal sıcaklıkları ve şekil fonksiyonları
dikdörtgen elemanlarda şu şekilde ifade edilirler:
 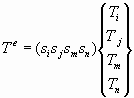 (4.11) (4.11)
Burada
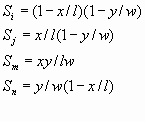 (4.12) (4.12)
eşitlikleri ile elde edilirler.
Galerkinin ısı difüzyon denklemi ele alındığında
, x,y lineer koordinat sisteminde ifade edilen denklem (4.10) dört sonuç verir.
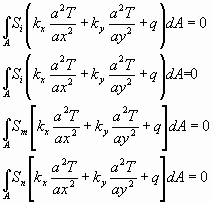
| 