|
SONLU ELEMANLAR YÖNTEMİ
Giriş
Sonlu elemanlar metodu matematikçilerden
ziyade daha çok mühendisler tarafından geliştirilmiştir. Metot
ilk olarak gerilme analizi problemlerine uygulanmıştır. Tüm bu
uygulamalarda bir büyüklük alanının hesaplanması
istenmektedir. Gerilme analizinde bu değer deplasman alanı veya gerilme
alanı; ısı analizinde sıcaklık alanı veya ısı
akısı; akışkan problemlerinde ise akım fonksiyonu veya
hız potansiyel fonksiyonudur. Hesaplanan büyüklük alanın almış
olduğu en büyük değer veya en büyük gradyen pratikte özel bir öneme
haizdir [Engin, A. ve ark.2000].
Sonlu elemanlar metodunda yapı, davranışı
daha önce belirlenmiş olan bir çok elemana bölünür. Elemanlar "nod"
adı verilen noktalarda tekrar birleştirilirler (Bak Şekil 3.46).
Bu şekilde cebrik bir denklem takımı elde edilir. Gerilme
analizinde bu denklemler nodlardaki denge denklemleridir. İncelenen
probleme bağlı olarak bu şekilde yüzlerce hatta binlerce denklem
elde edilir. Bu denklem takımının çözümü ise bilgisayar
kullanımını zorunlu kılmaktadır.
Sonlu elemanlar metodunda temel fikir sürekli fonksiyonları
bölgesel sürekli fonksiyonlar (genellikle polinomlar) ile temsil etmektir.
Bunun anlamı bir eleman içerisinde hesaplanması istenen büyüklüğün
(örneğin deplasmanın) değeri o elemanın nodlarındaki
değerler kullanılarak interpolasyon ile bulunur.
Bu nedenle sonlu elemanlar metodunda bilinmeyen ve hesaplanması istenen değerler
nodlardaki değerlerdir. Bir varyasyenel prensip (örneğin; enerjinin
minimum olması prensibi) kullanılarak büyüklük alanının
nodlardaki değerleri için bir denklem takımı elde
edilir. Bu denklem takımının matris formundaki gösterimi
[K] . [D] = [R]
şeklindedir. Burada [D] büyüklük alanının
nodlardaki bilinmeyen değerlerini temsil eden vektör, [R] bilinen yü k
vektörü ve [K] ise bilinen sabitler matrisidir. Gerilme analizinde [K]
rijitlik matrisi olarak bilinmektedir.
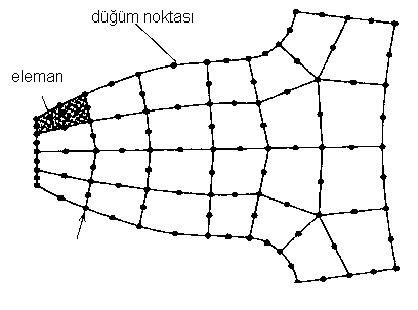
Şekil 3.46 Bir
sonlu eleman modelinde nod noktaları ve elemanlar
4.2 Sonlu Elemanlar Metodunun Tarihsel Gelişimi
Sonlu elemanlar metodu ilk olarak yapı analizinde kullanılmaya
başlandı. İlk çalışmalar Hrennikoff (1941) ve Mc Henry
(1943) tarafından geliştirilen yarı analitik analiz metotlarıdır.
Argyis ve Kelsey (1960) virtuel iş prensibini kullanarak bir direkt yaklaşım
metodu geliştirmiştir. Turner ve diğerleri (1956) bir üçgen
eleman için rijitlik matr isini oluşturmuştur.
"Sonlu Elemanlar" terimi ilk defa Clough (1960) tarafından çalışmasında
telâffuz edilmiştir. Metodun üç- boyutlu problemlere uygulanması
iki-boyutlu teoriden sonra kolayca gerçeklenmiştir (örneğin, Argyis
(1964)).
İlk gerçek kabuk elemanlar eksenel simetrik elemanlar
olup (Grafton ve Strome (1963)), bunları silindirik ve diğer kabuk
elemanları izlemiştir (Gallagher (1969)). Araştırıcılar
1960'lı yılların başlarında non-lineer problemlerle
ilgilenmeye başladılar. Turner ve diğerleri ( 1960)
geometrik olarak non-lineer problemler için bir çözüm tekniği geliştirdi.
Sonlu elemanlar metoduyla stabilite analizi ise ilk Martin (1965) tarafından
tartışılmıştır. Statik problemlerin yanısıra
dinamik problemlerde sonlu elemanlar metoduyla incelenmeye
başlandı (Zienkiewicz ve diğerleri (1966) ve Koening ve Davids
(1969)). 1943 yılında Courant bölgesel sürekli lineer yaklaşım
kullanarak bir burulma problemi için çözüm üretmiştir.
Yapı alanı dışındaki problemlerin
sonlu elemanlar metoduyla çözümü 1960 'lı yıllarda başlamıştır.
Örneğin Zienkiewicz ve Cheung (1965) sonlu elemanlar metodu ile Poisson
denklemini çözmüştür. Doctors (1970) ise metodu potansiyel akışa
uygulamıştır. Sonlu elemanlar metodu geliştirilerek ısı
transferi, yeraltı sularının a kışı,
manyetik alan ve diğer bir çok alana uygulanmaktadır.
Genel amaçlı sonlu elemanlar paket programları
1970'li yıllardan itibaren ortaya çıkmaya başlamıştır.
1980'li yılların sonlarına doğru ise artık paket
programlar mikro bilgisayarlarda kullanılmaya başlandı. 1990 yıllarının
ortaları itibarîyle sonlu elemanlar metodu ve uygulamalarıyla ilgili
yaklaşık olarak 40.000 makale ve kitap yayınlanmıştır.
4.3 Sonlu Elemanlarla Modelleme
4.3.1 Genel Olarak Modelleme
Modelleme bir fiziksel yapı veya sürecin analitik veya
sayısal olarak yeniden inşa edilmesidir. Sonlu elemanlar metodunda
modelleme basitçe nod ve elemanlardan oluşan bir ağ yapısı
hazırlamak değildir. Problemi gerekli şekilde modelleyebilmek için
gerekli sayı ve tipteki elemana karar vermek ancak
problemin fiziğinin iyi şekilde anlaşılmasıyla mümkündür.
Kötü şekil verilmiş elemanlar ile hesaplanması istenilen büyüklüğün
hesaplama alanı içindeki değişimini yansıtamayacak kadar büyük
boyutlu elemanlar modellemede istenmez. Şekil 3.47 de elemanlarda
genelde müsaade edilebilecek geometrik biçim bozukluklarının
seviyesi gösterilmektedir. Diğer yandan zaman ve bilgisayar olanaklarını
boş yere harcamamıza neden olacak, gereksiz kadar çok sayıda
elemanlardan oluşan bir modellemede istenmemektedir.
Hesaplanması istenilen büyüklüğü ve hesaplama alanı içindeki
değişimini yeterli doğrulukta verecek kadar sıklıkta
bir eleman dağılımına ihtiyaç vardır. Örneğin
Şekil 3.48 'de silindirik yüzeylerin modellenmesi için 4 nodlu veya 8
nodlu dört kenarlı elemanlar kullanılması
durumunda tipik bir eleman dağılımı gösterilmiştir. Diğer
yandan Şekil 3.49' de bir delik etrafında olması gereken tipik
eleman dağılımı görülmektedir. Hesaplanan değerlerin
kabul edilebilir olup olmadıklarının kontrol edilmesi ayrı bir
öneme sahiptir. Dikkat edilmesi gereken hususlar aşağıda kısaca
belirtilecektir.
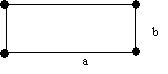
uzunluk oranı a/b için
genelde
10:1 oranına kadar müsaade edilebilir.
|
b < 15° 4 nodlu dört
kenarlı elemanlar için
b < 30° 8 nodlu dörtgen elemanlar
|

|
|
Şekil 3.48
Bir silindirik yüzey etrafındaki tipik eleman dağılımı. |
|
|
|
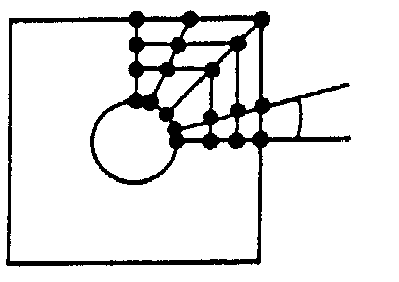
Şekil 3.49 Bir delikli geometride delik etrafındaki
tipik eleman dağılımı |
Devami ..
| 